Overview
In the previous chapter we explored a few ways that numbers can be represented in a digital computer, but we only briefly touched upon arithmetic operations that can be performed on those numbers. In this chapter we cover four basic arithmetic operations: addition, subtraction, multiplication, and division. We begin by describing how these four operations can be performed on fixed point numbers, and continue with a description of how these four operations can be performed on floating point numbers.
Some of the largest problems, such as weather calculations, quantum mechanical simulations, and land-use modeling, tax the abilities of even today’s largest computers. Thus the topic of high-performance arithmetic is also important. We conclude the chapter with an introduction to some of the algorithms and techniques used in speeding arithmetic operations.
The addition of binary numbers and the concept of overflow were briefly dis- cussed in Chapter 2. Here, we cover addition and subtraction of both signed and unsigned fixed point numbers in detail. Since the two’s complement representation of integers is almost universal in today’s computers, we will focus primarily on two’s complement operations. We will briefly cover operations on 1’s complement and BCD numbers, which have a foundational significance for other areas of computing, such as networking (for 1’s complement addition) and hand-held calculators (for BCD arithmetic.)
TWO’S COMPLEMENT ADDITION AND SUBTRACTION
In this section, we look at the addition of signed two’s complement numbers. As we explore the addition of signed numbers, we also implicitly cover subtraction as well, as a result of the arithmetic principle:
a - b = a + (-b).
We can negate a number by complementing it (and adding 1, for two’s complement), and so we can perform subtraction by complementing and adding. This results in a savings of hardware because it avoids the need for a hardware subtractor. We will cover this topic in more detail later.
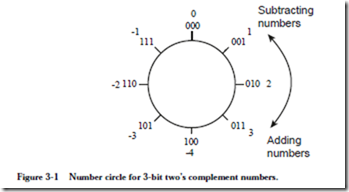
We will need to modify the interpretation that we place on the results of addition when we add two’s complement numbers. To see why this is the case, consider Figure 3-1. With addition on the real number line, numbers can be as large or as
small as desired—the number line goes to ±¥, so the real number line can accommodate numbers of any size. On the other hand, as discussed in Chapter 2, computers represent data using a finite number of bits, and as a result can only store numbers within a certain range. For example, an examination of Table 2.1 shows that if we restrict the size of a number to, for example, 3 bits, there will only be eight possible two’s complement values that the number can assume. In Figure 3-1 these values are arranged in a circle beginning with 000 and proceeding around the circle to 111 and then back to 000. The figure also shows the decimal equivalents of these same numbers.
Some experimentation with the number circle shows that numbers can be added or subtracted by traversing the number circle clockwise for addition and counterclockwise for subtraction. Numbers can also be subtracted by two’s complementing the subtrahend and adding. Notice that overflow can only occur for addition when the operands (“addend” and “augend”) are of the same sign. Furthermore, overflow occurs if a transition is made from +3 to -4 while proceeding around the number circle when adding, or from -4 to +3 while subtracting. (Two’s complement overflow is discussed in more detail later in the chapter.)
Here are two examples of 8-bit two’s complement addition, first using two positive numbers:
The carry produced by addition at the highest (leftmost) bit position is discarded in two’s complement addition. A similar situation arises with a carry out of the highest bit position when adding two negative numbers:
The carry out of the leftmost bit is discarded because the number system is modular—it “wraps around” from the largest positive number to the largest negative number as Figure 3-1 shows.
Although an addition operation may have a (discarded) carry-out from the MSB, this does not mean that the result is erroneous. The two examples above yield correct results in spite of the fact that there is a carry-out of the MSB. The next section discusses overflow in two’s complement addition in more detail.
Overflow
When two numbers are added that have large magnitudes and the same sign, an overflow will occur if the result is too large to fit in the number of bits used in the representation. Consider adding (+80)10 and (+50)10 using an eight bit for- mat. The result should be (+130)10, however, as shown below, the result is (-126)10:
This should come as no surprise, since we know that the largest positive 8-bit two’s complement number is +(127)10, and it is therefore impossible to represent (+130)10. Although the result 100000102 “looks” like 13010 if we think of it in unsigned form, the sign bit indicates a negative number in the signed form, which is clearly wrong.
In general, if two numbers of opposite signs are added, then an overflow cannot occur. Intuitively, this is because the magnitude of the result can be no larger than the magnitude of the larger operand. This leads us to the definition of two’s complement overflow:
If the numbers being added are of the same sign and the result is of the opposite sign, then an overflow occurs and the result is incorrect. If the numbers being added are of opposite signs, then an overflow will never occur. As an alternative method of detecting overflow for addition, an overflow occurs if and only if the carry into the sign bit differs from the carry out of the sign bit.
If a positive number is subtracted from a negative number and the result is positive, or if a negative number is subtracted from a positive number and the result is negative, then an overflow occurs. If the numbers being subtracted are of the same sign, then an overflow will never occur.
HARDWARE IMPLEMENTATION OF ADDERS AND SUBTRACTORS
Up until now we have focused on algorithms for addition and subtraction. Now we will take a look at implementations of simple adders and subtractors.
Ripple-Carry Addition and Ripple-Borrow Subtraction
In Appendix A, a design of a four-bit ripple-carry adder is explored. The adder is modeled after the way that we normally perform decimal addition by hand, by summing digits in one column at a time while moving from right to left. In this section, we review the ripple-carry adder, and then take a look at a ripple-borrow subtractor. We then combine the two into a single addition/subtraction unit.
Figure 3-2 shows a 4-bit ripple-carry adder that is developed in Appendix A. Two
binary numbers A and B are added from right to left, creating a sum and a carry at the outputs of each full adder for each bit position.
Four 4-bit ripple-carry adders are cascaded in Figure 3-3 to add two 16-bit numbers. The rightmost full adder has a carry-in of 0. Although the rightmost full adder can be simplified as a result of the carry-in of 0, we will use the more general form and force c0 to 0 in order to simplify subtraction later on.
Subtraction of binary numbers proceeds in a fashion analogous to addition. We can subtract one number from another by working in a single column at a time, subtracting digits of the subtrahend bi, from the minuend ai, as we move from right to left. As in decimal subtraction, if the subtrahend is larger than the minuend or there is a borrow from a previous digit then a borrow must be propagated
trates a four-bit ripple-borrow subtractor that is made up of four full subtractors.
As discussed above, an alternative method of implementing subtraction is to form the two’s complement negative of the subtrahend and add it to the minuend. The circuit that is shown in Figure 3-6 performs both addition and subtrac-
tion on four-bit two’s complement numbers by allowing the bi inputs to be complemented when subtraction is desired. An ADD /SUBTRACT control line determines which function is performed. The bar over the ADD symbol indicates the ADD operation is active when the signal is low. That is, if the control line is 0, then the ai and bi inputs are passed through to the adder, and the sum is generated at the si outputs. If the control line is 1, then the ai inputs are passed through to the adder, but the bi inputs are one’s complemented by the XOR gates before they are passed on to the adder. In order to form the two’s complement negative, we must add 1 to the one’s complement negative, which is accomplished by setting the carry_in line (c0) to 1 with the control input. In this way, we can share the adder hardware among both the adder and the subtractor.
ONE’S COMPLEMENT ADDITION AND SUBTRACTION
Although it is not heavily used in mainstream computing anymore, the one’s complement representation was used in early computers. One’s complement addition is handled somewhat differently from two’s complement addition: the carry out of the leftmost position is not discarded, but is added back into the least significant position of the integer portion as shown in Figure 3-7. This is
number circle has two positions for 0. When we add two numbers, if we traverse through both -0 and +0, then we must compensate for the fact that 0 is visited twice. The end-around carry advances the result by one position for this situation.
Notice that the distance between -0 and +0 on the number circle is the distance between two integers, and is not the distance between two successive represent- able numbers. As an illustration of this point, consider adding (5.5)10 and
(-1.0)10 in one’s complement arithmetic, which is shown in Figure 3-9. (Note that we can also treat this as a subtraction problem, in which the subtrahend is negated by complementing all of the bits, before adding it to the minuend.) In
order to add (+5.5)10 and (-1.0)10 and obtain the correct result in one’s complement, we add the end-around carry into the one’s position as shown. This adds complexity to our number circle, because in the gap between +0 and -0, there are valid numbers that represent fractions that are less than 0, yet they appear on the number circle before -0 appears. If the number circle is reordered to avoid this anomaly, then addition must be handled in a more complex manner.
The need to look for two different representations for zero, and the potential need to perform another addition for the end-around carry are two important reasons for preferring the two’s complement arithmetic to one’s complement arithmetic.